Support Vector Machines

Support Vector Machines

A Support Vector Machine (SVM) is a powerful supervised machine learning model used for classification. An SVM makes classifications by defining a decision boundary and then seeing what side of the boundary an unclassified point falls on. Decision boundaries get defined,  by using a training set of classified points.  

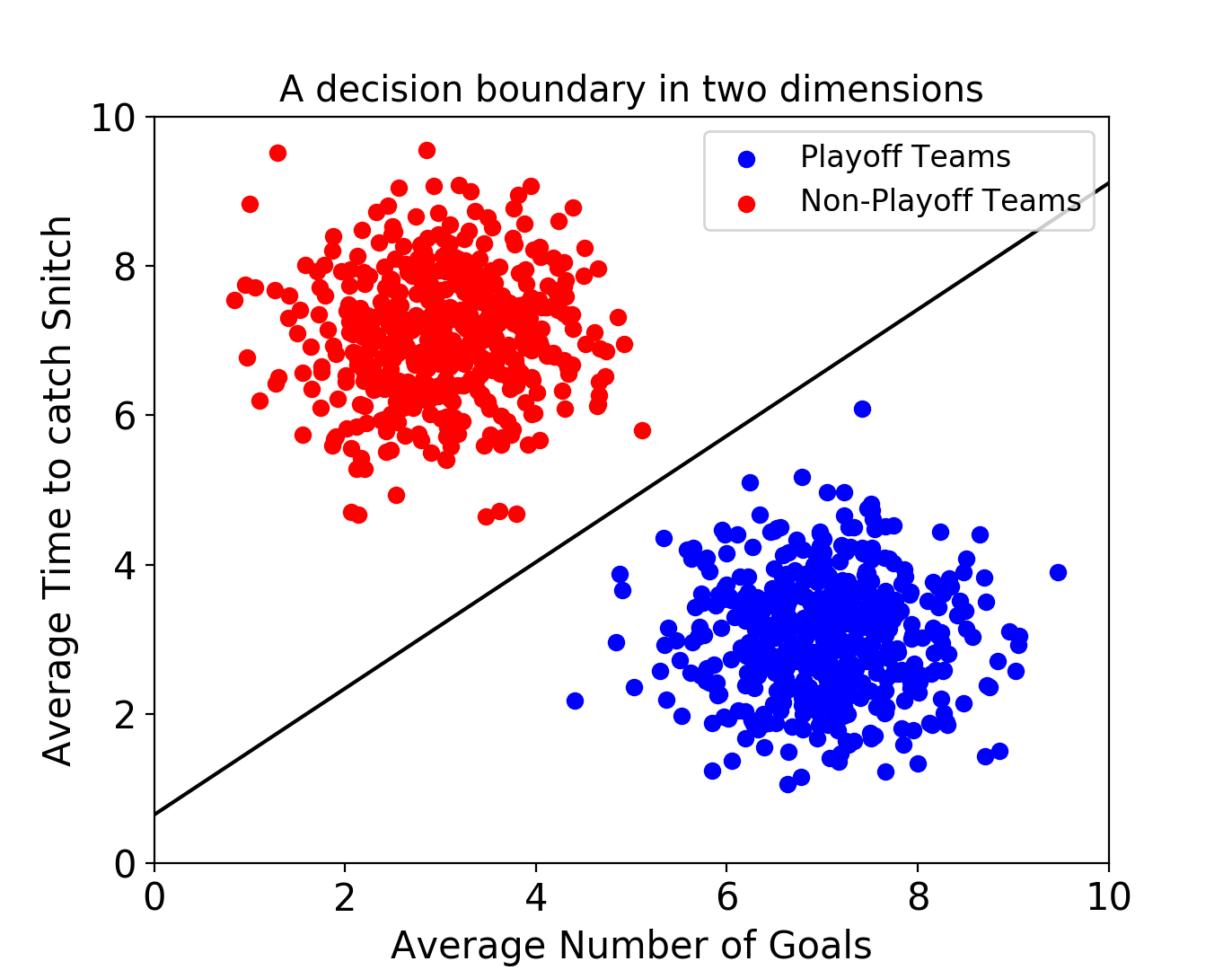
Two clusters of points separated by a line 

Decision boundaries exist even when your data has more than two features. If there are three features, the decision boundary is now a plane rather than a line.

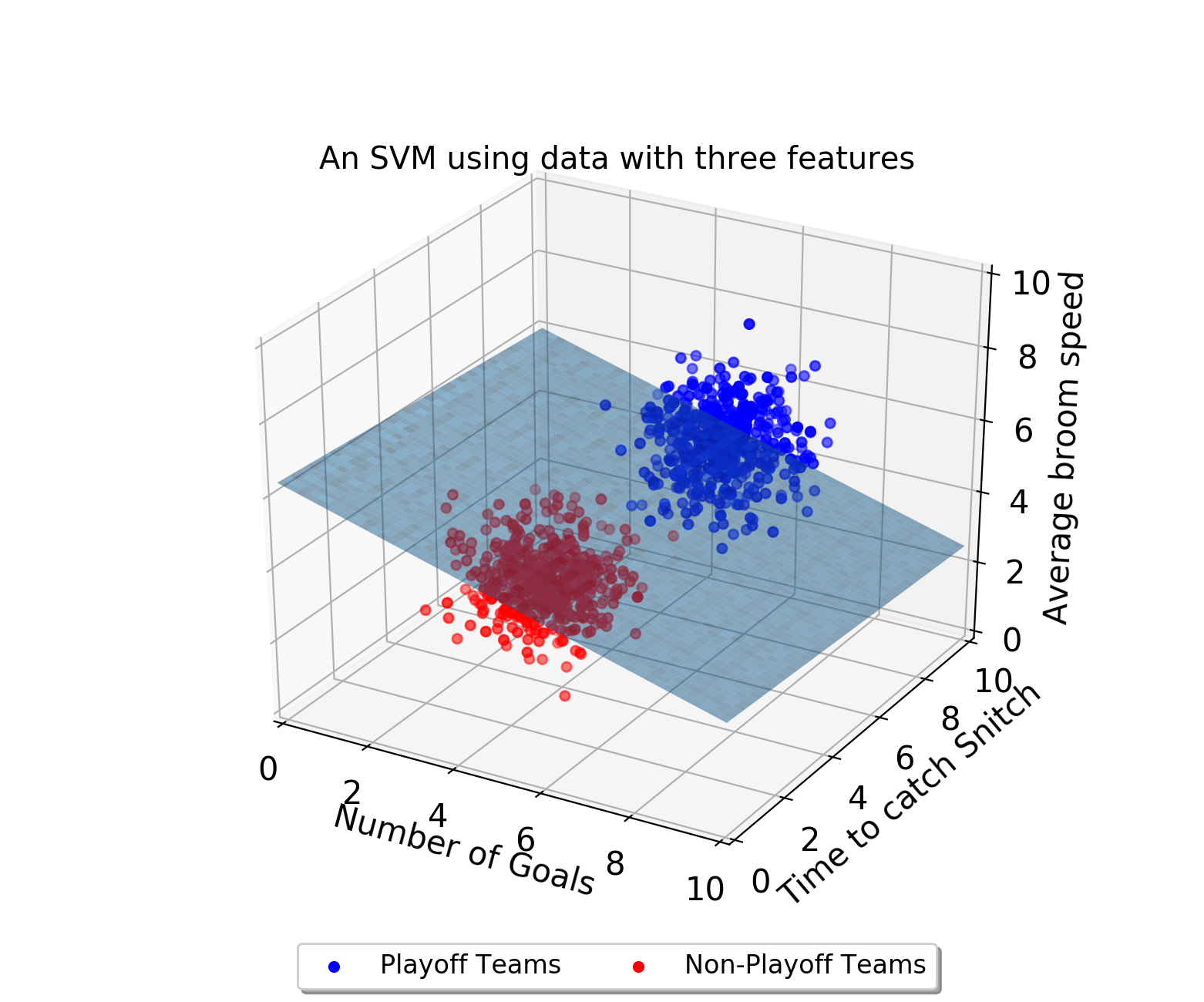
Two clusters of points in three dimensions separated by a plane. 

As the number of dimensions grows past 3, it becomes very difficult to visualize these points in space. Nonetheless, SVMs can still find a decision boundary. However, rather than being a separating line, or a separating plane, the decision boundary is called a separating hyperplane.



Optimal Decision Boundaries

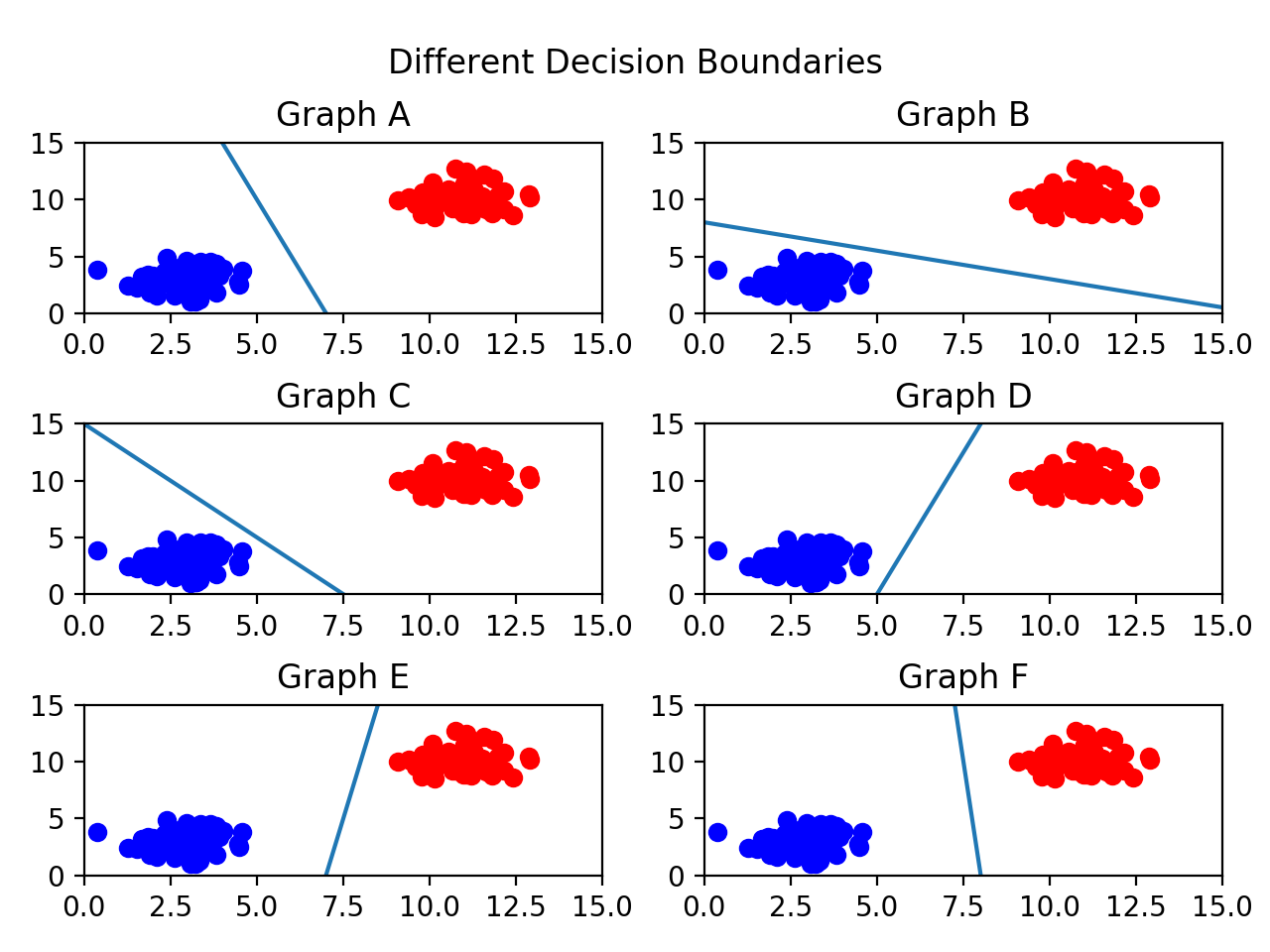
In general, we want our decision boundary to be as far away from training points as possible. Maximizing the distance between the decision boundary and points in each class will decrease the chance of false classification.

6 different valid decision boundaries


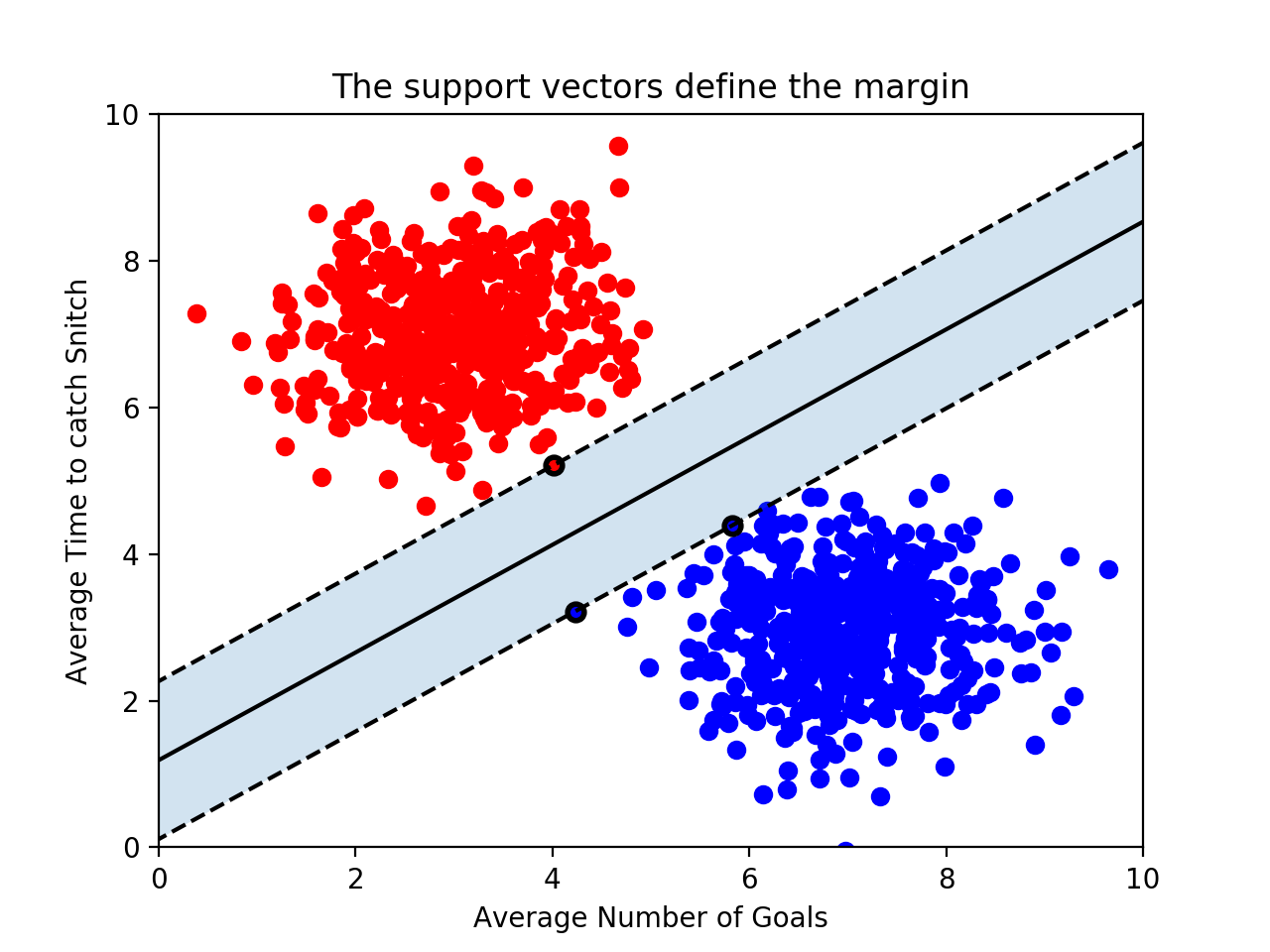
Support Vectors and Margins

 The support vectors are the points in the training set closest to the decision boundary. In fact, these vectors are what define the decision boundary.

The distance between a support vector and the decision boundary is called the margin.  

decision boundary with margin highlighted 

Outliers

 SVMs try to maximize the size of the margin while still correctly separating the points of each class. As a result, outliers can be a problem.

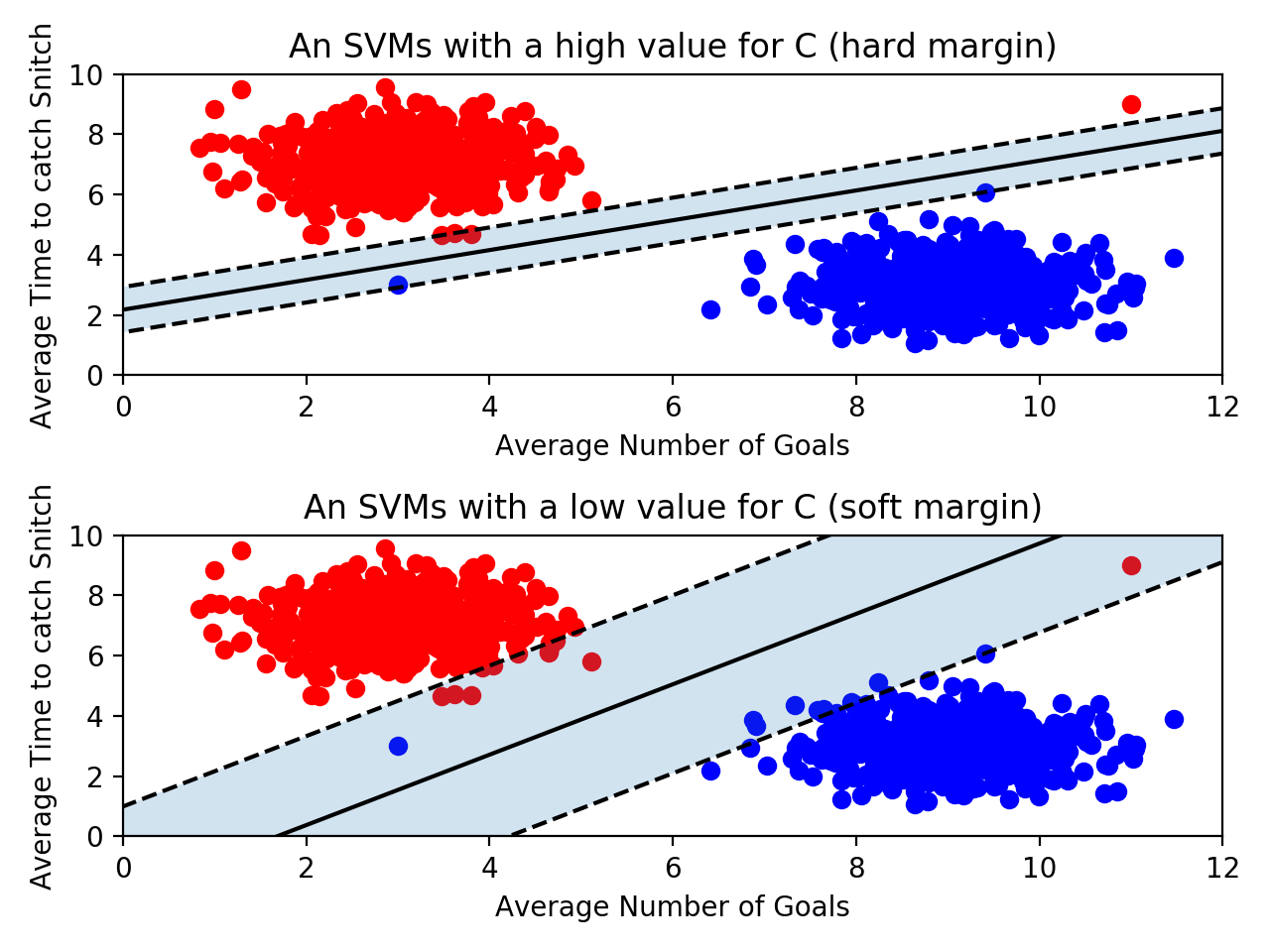
One graph with a hard margin and one graph with a soft margin 

SVMs have a parameter C that determines how much error the SVM will allow for. If C is large, then the SVM has a hard margin — it won’t allow for many misclassifications, and as a result, the margin could be fairly small. If C is too large, the model runs the risk of overfitting. It relies too heavily on the training data, including the outliers.

On the other hand, if C is small, the SVM has a soft margin. Some points might fall on the wrong side of the line, but the margin will be large. This is resistant to outliers, but if C gets too small, you run the risk of underfitting. The SVM will allow for so much error that the training data won’t be represented.

When using scikit-learn’s SVM, you can set the value of C when you create the object:

classifier = SVC(C = 0.01)



 



 





Kernels

 
 Up to this point, we have been using data sets that are linearly separable. This means that it’s possible to draw a straight decision boundary between the two classes. However, what would happen if an SVM came along a dataset that wasn’t linearly separable?

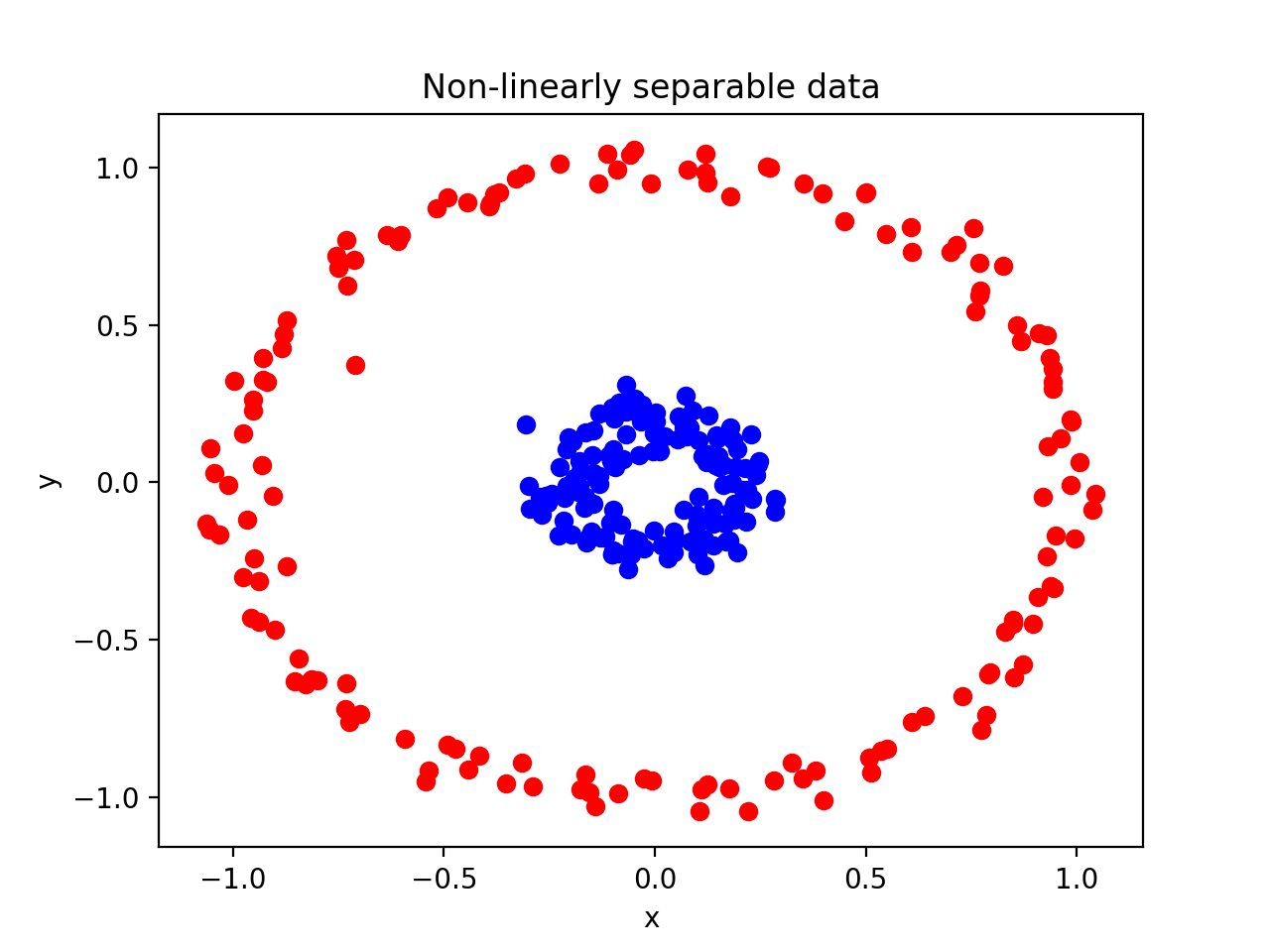
data points clustered in concentric circles 
when we set kernel = 'linear' when creating our SVM? Kernels are the key to creating a decision boundary between data points that are not linearly separable.

Polynomial Kernel

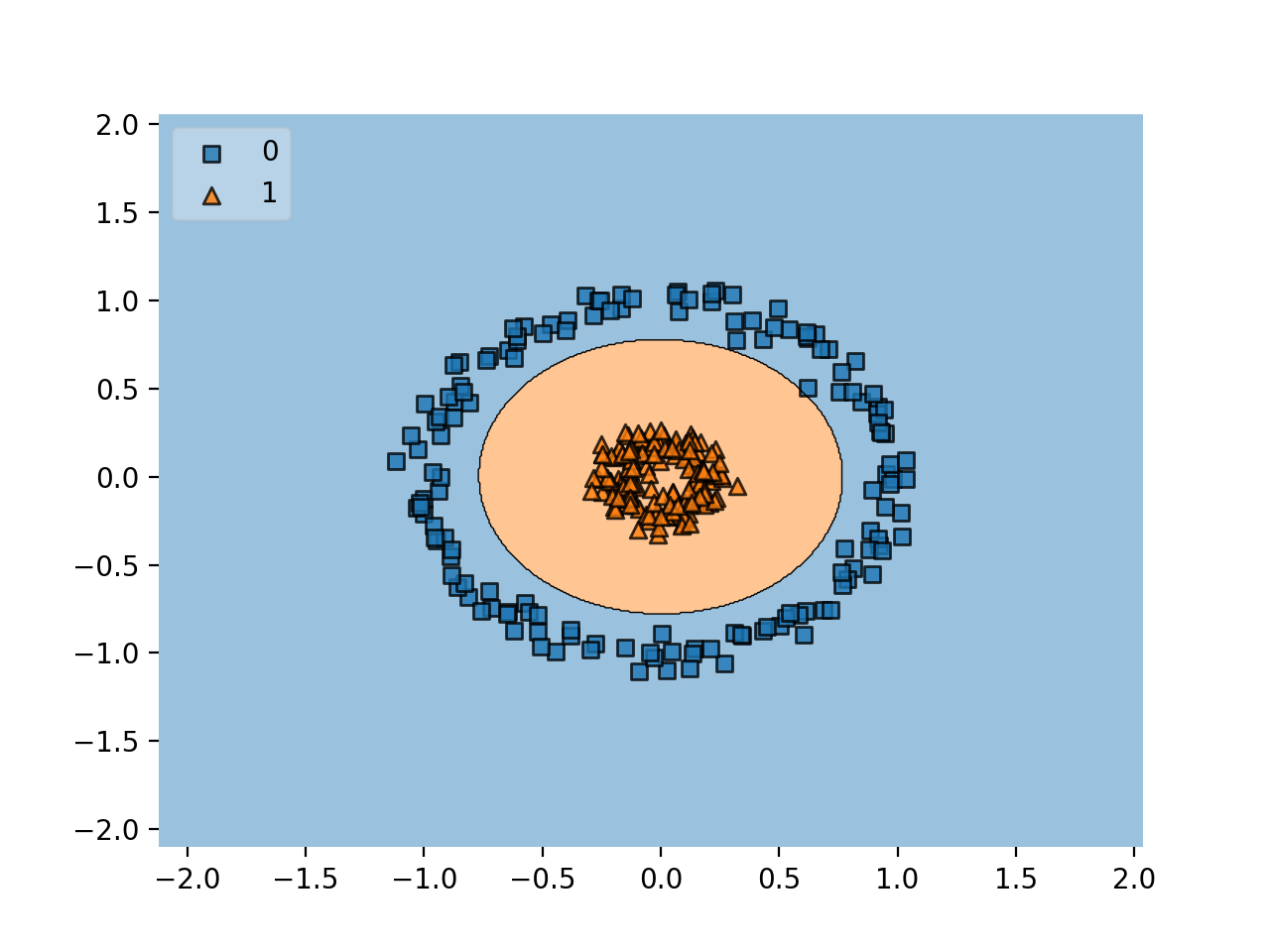
 By projecting the data into a higher dimension, the two classes are now linearly separable by a plane. We could visualize what this plane would look like in two dimensions to get the following decision boundary.
The decision boundary is a circle around the inner points. 


Radial Bias Function Kernel

The most commonly used kernel in SVMs is a radial basis function (rbf) kernel. This is the default kernel used in scikit-learn’s SVC object. If you don’t specifically set the kernel to "linear", "poly" the SVC object will use an rbf kernel. If you want to be explicit, you can set kernel = "rbf", although that is redundant.

The polynomial kernel we used transformed two-dimensional points into three-dimensional points. An rbf kernel transforms two-dimensional points into points with an infinite number of dimensions!

it is important to know about the rbf kernel’s gamma parameter. 

classifier = SVC(kernel = "rbf", gamma = 0.5, C = 2)
gamma is similar to the C parameter. You can essentially tune the model to be more or less sensitive to the training data. A higher gamma, say 100, will put more importance on the training data and could result in overfitting. Conversely, A lower gamma like 0.01 makes the points in the training data less relevant and can result in underfitting.


Comments

Post a Comment

Popular posts from this blog

ACCURACY, RECALL, PRECISION, F1 SCORE

ACCURACY, RECALL, PRECISION, F1 SCORE Classifying a single point can result in a true positive ( truth = 1 , guess = 1 ), a true negative ( truth = 0 , guess = 0 ), a false positive ( truth = 0 , guess = 1 ), or a false negative ( truth = 1 , guess = 0 ). Accuracy measures how many classifications your algorithm got correct out of every classification it made. Recall measures the percentage of the relevant items your classifier was able to successfully find. Precision measures the percentage of items your classifier found that were actually relevant. Precision and recall are tied to each other. As one goes up, the other will go down. F1 score is a combination of precision and recall. F1 score will be low if either precision or recall is low. The decision to use precision, recall, or F1 score ultimately comes down to the context of your classification. Maybe you don’t care if your classifier has a lot of false positives. If that’s the case, precision doesn’t matter as m...
Read more

Random Forest

RANDOM FOREST A random forest is an ensemble machine learning model. It makes a classification by aggregating the classifications of many decision trees. Random forests are used to avoid overfitting. By aggregating the classification of multiple trees, having overfitted trees in a random forest is less impactful. Every decision tree in a random forest is created by using a different subset of data points from the training set. Those data points are chosen at random with replacement , which means a single data point can be chosen more than once. This process is known as bagging . When creating a tree in a random forest, a randomly selected subset of features are considered as candidates for the best splitting feature. If your dataset has n features, it is common practice to randomly select the square root of n features. Boosting Steps : Draw a random subset of training samples d1 without replacement from the training set D to train a weak learner C1 ...
Read more